Fórmula de Herón
Demostración
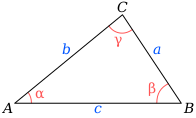
Una demostración moderna, que emplea álgebra y trigonometría (bastante distinta a la que dio Herón en su libro), podría ser la siguiente. Sea un triángulo de lados a, b, c, cuyos ángulos opuestos a cada uno de esos lados son Entonces, por el teorema del coseno:
Entonces, por el teorema del coseno: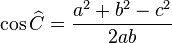 .
.
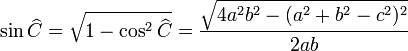 .
.

 , se llega finalmente a:
, se llega finalmente a:Generalizaciones
La fórmula de Herón es un caso particular de la fórmula de Brahmagupta para el cálculo del área de cuadriláteros inscritos en una circunferencia; y ambas son casos particulares de la fórmula de Bretschneider para calcular área de un cuadrilátero.Expresando la fórmula de Herón de forma matricial dentro de un determinante en términos de cuadrados de distancias de los tres vértices dados, obtenemos:
Así como un triángulo está determinado por las longitudes de sus tres lados, un tetraedro lo está por las longitudes de sus seis lados. Tartaglia halló la fórmula del volumen del tetraedro en función de las longitudes de sus lados. Los determinantes de Cayley-Menger generalizan esta fórmula a dimensiones por encima de tres.





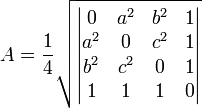
No hay comentarios:
Publicar un comentario